Quando iniciamos um aplicativo, site, sistema, ou diversos outros ambientes de interação, o primeiro passo é criar diferentes tipos de propostas de como vai ser a aplicação e de como vai ser seu comportamento. Se você é desenvolvedor, independente de ser designer ou programador, ou ainda está estudando, você já deve ter tido a necessidade de criar, ao menos, um rascunho de como será a interface gráfica de sua aplicação. E, se você pretende trabalhar especificamente com interfaces gráficas ou UX, a definição desses termos é ainda mais importante, sendo fundamental para uma boa comunicação e escolha de ferramentas adequadas.
Importância
Quando o desenvolvedor está em reunião com seu cliente, ou apenas lendo os requerimentos, este já vislumbra em sua mente o processo pelo qual o usuário conseguirá atingir seu objetivo. Além disso, também pensa em como comandos e dados devem influenciar uns aos outros (o que chamamos de regra de negócio do software). Mas nossa mente não é exatamente o melhor local para armazenar informações, pois a memória humana é volátil, se adapta e, o que é mais comum, se esquece de informações que podem ser importantes.

Por isso, é normal que um profissional, desde o seu primeiro pensamento, já comece a fazer rabiscos e anotações em uma caderneta ou em um guardanapo. Dessa forma, ele vai poder planejar não apenas o leiaute, mas todo comportamento do usuário e, inclusive, ajudar a modelagem de dados e lógica do projeto.
Esboços ou Sketchs
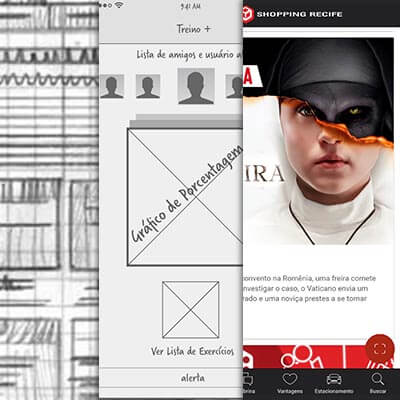
Um esboço ou sketch, é o primeiro passo para a criação da interface gráfica de um aplicativo. Basicamente é o que o desenvolvedor em primeiro passo. Desenhos simples, com muitas marcações, textos e números, que devem ser suficientes apenas para a compreensão deste e/ou do designer responsável (caso o designer não seja o próprio desenvolvedor). Esses esboços são feitos em papel, de preferência em um bloco de anotações, com lapiseira ou caneta. Fazer à mão é importante para que a fluidez do pensamento resolva melhores definições, assim como a ideia flui melhor dentro da cabeça de que o está projetando.
Para quem tem uma frequência muito alta de rascunhos, existem cadernetas específicas para isso, tendo formatos e linhas de base adequadas para o tipo de dispositivo. Outras pessoas preferem andar com papéis impressos com os templates base. Sites como o SneakPeekit e o PaperBrowser, disponibilizam templates para esboços.

Wireframes
Wireframes são leiautes demonstrativos da diagramação de elementos na tela, geralmente contendo indicadores. Trata-se de uma evolução de um esboço, sendo mais bem trabalhado, indicando a disposição dos diversos elementos e conteúdo. Por originalmente serem desenhados em papeis milimetrados ou pautados, são também chamados de esboços de grade. Esta etapa ainda pode ser feita por alguém sem muita experiência com design, pois é basicamente uma forma de organizar as ideias rabiscadas anteriormente no papel. Se você designer, é comum pular essa etapa, indo do esboço direto para o mockup.
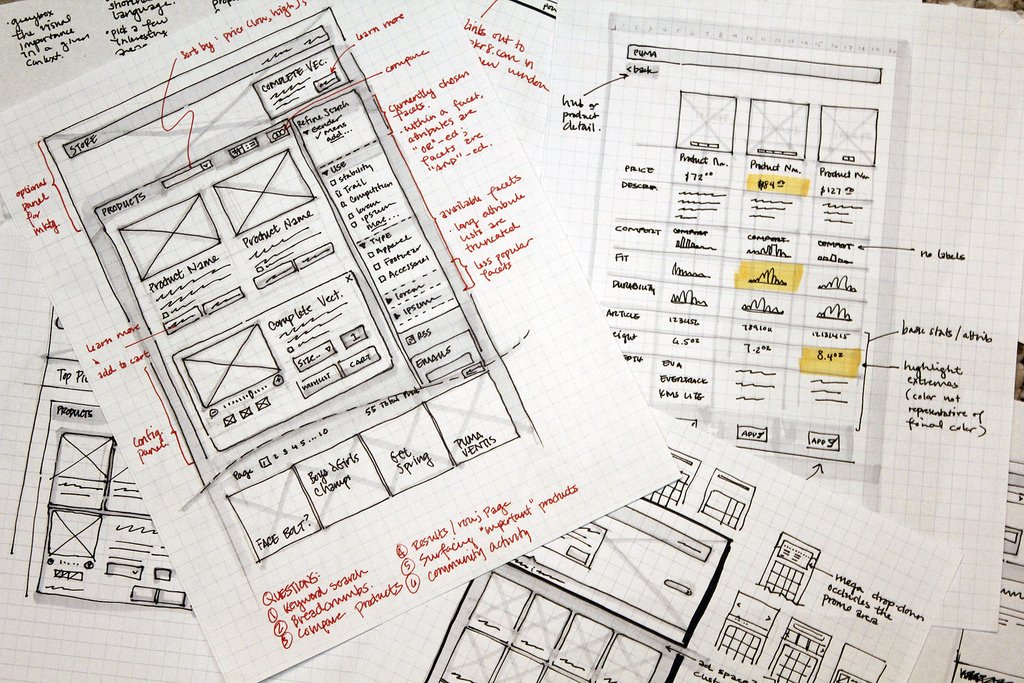
Hoje os wireframes são feitos digitalmente, por ferramentas específicas, como o Balsamiq Wireframes ou através de conjuntos de bibliotecas e plugins que podem ser incorporados aos aplicativos da Adobe, como o Illustrator.
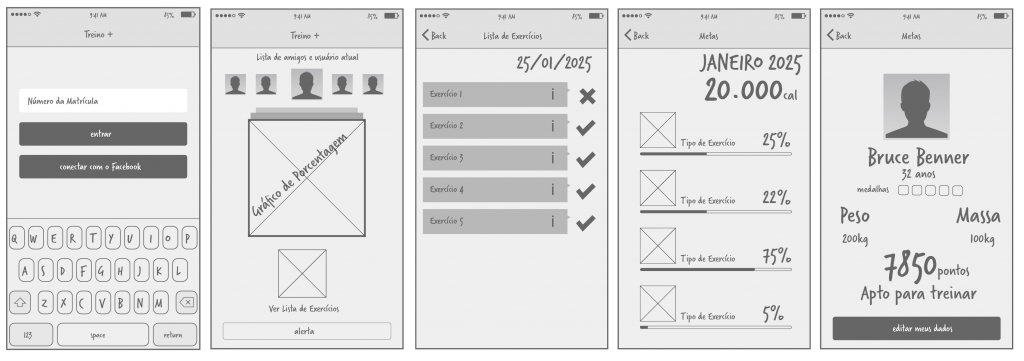
Mockups
Agora é a vez do designer (ou seu lado designer) brilhar. Os mockups são leiautes com exemplos finais, ou muito próximo destes, da interface gráfica. Basicamente serve de mapa para a implementação da mesma, com exemplos das telas, componentes e estilos já finalizados. Os mockups são bem mais trabalhados que os wireframes e raramente possuem indicadores internos, para não atrapalhar a compreensão da GUI (Interface Gráfica do Usuário). Muitas vezes, é comum mostrar os mockups também em cenas de interações, ajudando a demonstrar o uso e a ter uma melhor ideia do resultado final.
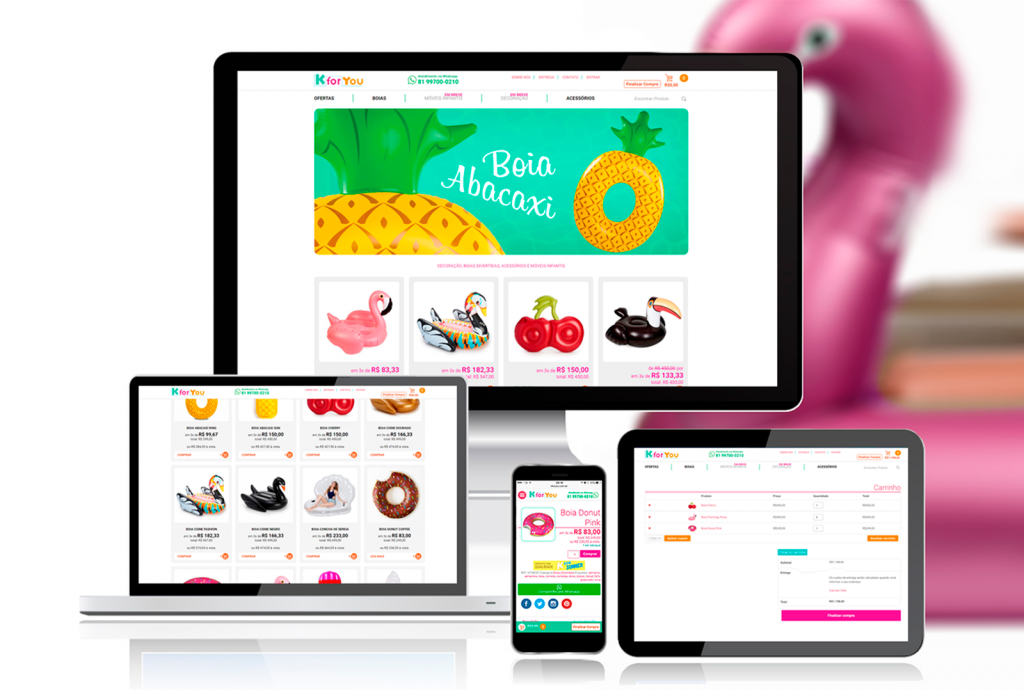
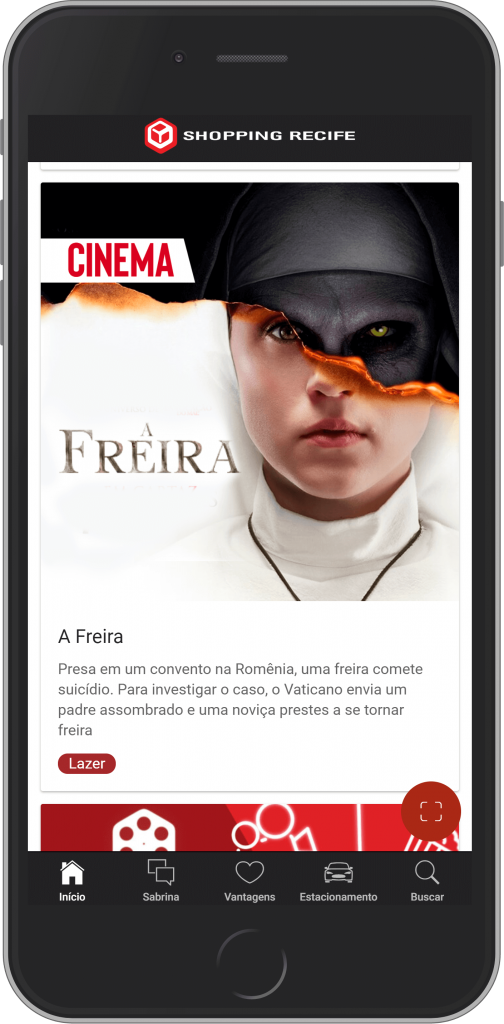
Dentre diversas ferramentas para criação de mockups, temos o Adobe XD (gratuito), o Sketch e há quem até hoje prefira criar bibliotecas no Photoshop, Illustrator, Pixelmator ou similares. Sendo opção ou não do designer seguir as diretrizes de interface humana recomendado para o sistema ou aplicação.
Human Interface Guidelines
Se você é designer, você ainda deve trabalhar no chamado Human Interface Guidelines ou Diretrizes de Interface Humana, como alguns gostam de chamar. Trata-se das instruções básicas de como deve ser a GUI da aplicação, de um contexto de uma suite agregada ou até mesmo, como em sistemas operacionais, instruções de como outros designers devem implementar soluções para essa aplicação.
Para quem já trabalha ou trabalhou com identidades visuais, se assemelha muito aos manuais destas, porém ainda mais detalhados, mas com as informações sobre espaçamentos, iconografia, tipografia, cores, etc, incluindo, mas não se resumindo, a um conjunto de mockups que possuem exemplos das telas. Essas informações devem ser seguidas à risca por quem for implementar, sejam outros designers ou programadores front-end.

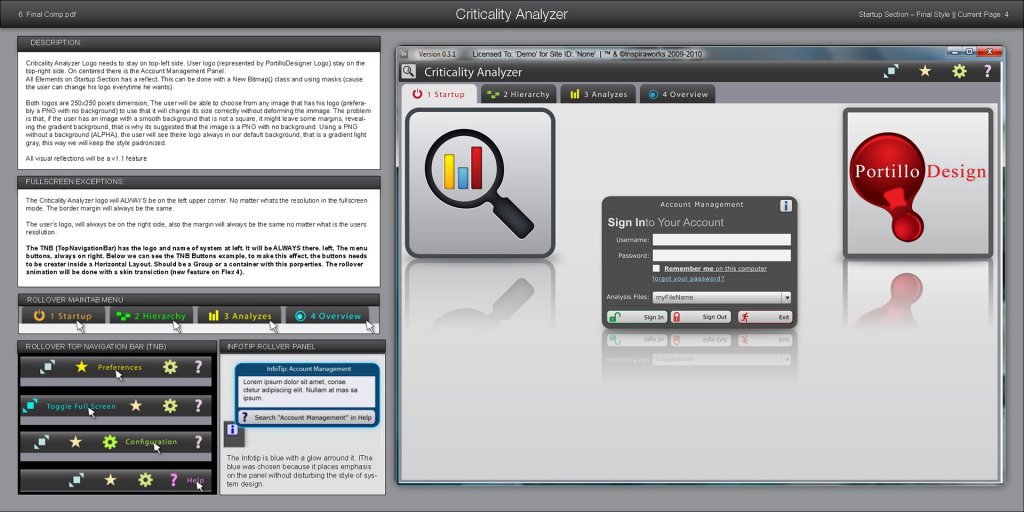
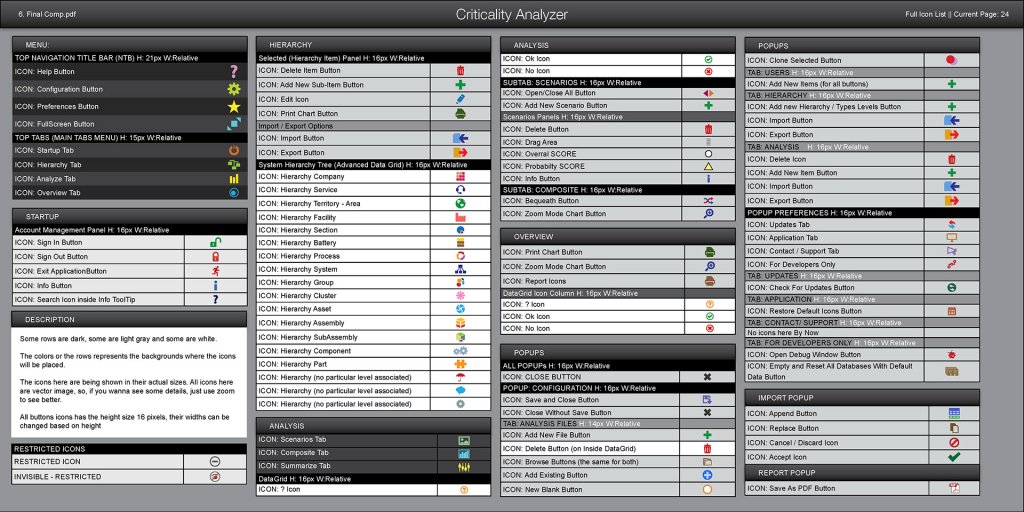
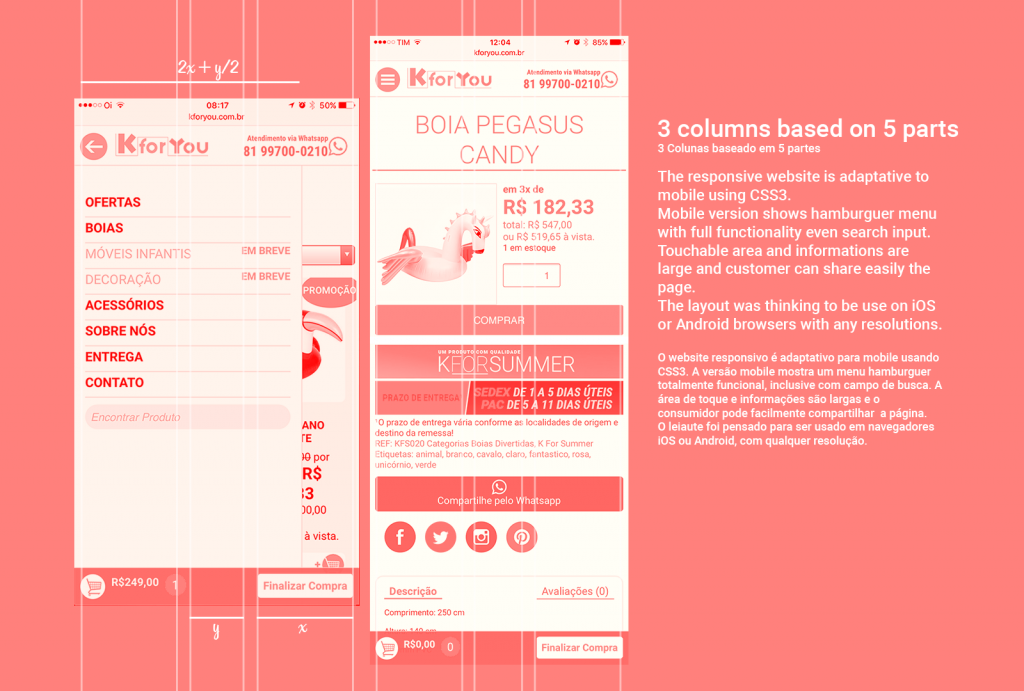
As Diretrizes são fundamentais principalmente em um sistema com uma quantidade de telas indefinida, como sistemas de gestão. Elas vão servir de guia para a criação de novas telas e componentes, além de inspiração para futuros materiais de publicidade e até sites.

Se você vai fazer uma aplicação para um determinado sistema operacional, ou apenas quer usar um como referência para não se preocupar tanto com o design, existem algumas diretrizes bem famosas, dentre elas a da Apple (disponível para iOS/MacOS/TVOS/WatchOS), o Material Design do Google (aplicável para sites e Android), o Fluent Design da Microsoft (também disponível o UXGuide legado) e tantos outros mais genéricos que você pode encontrar ou comprar pela internet.
UI Kits
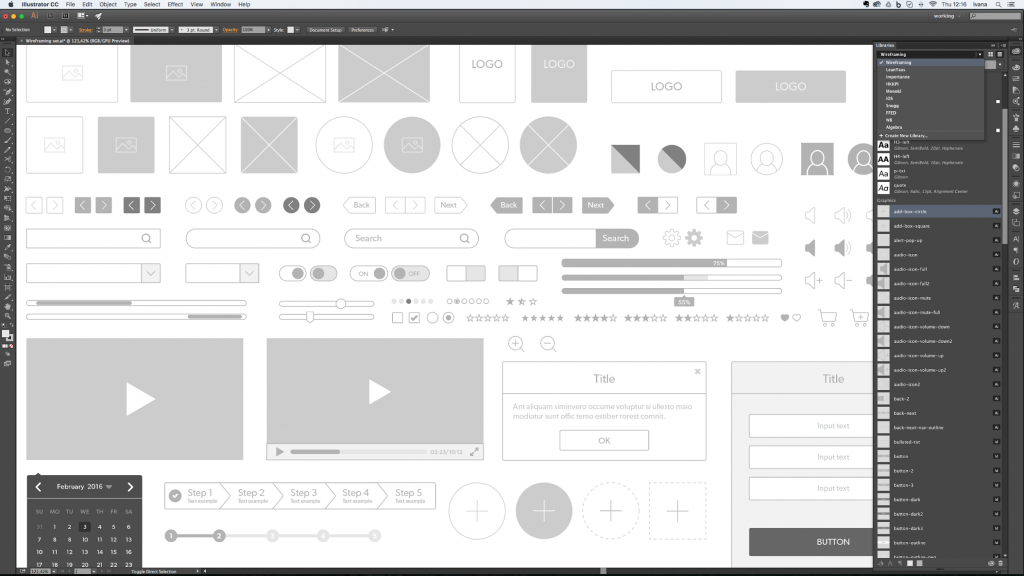
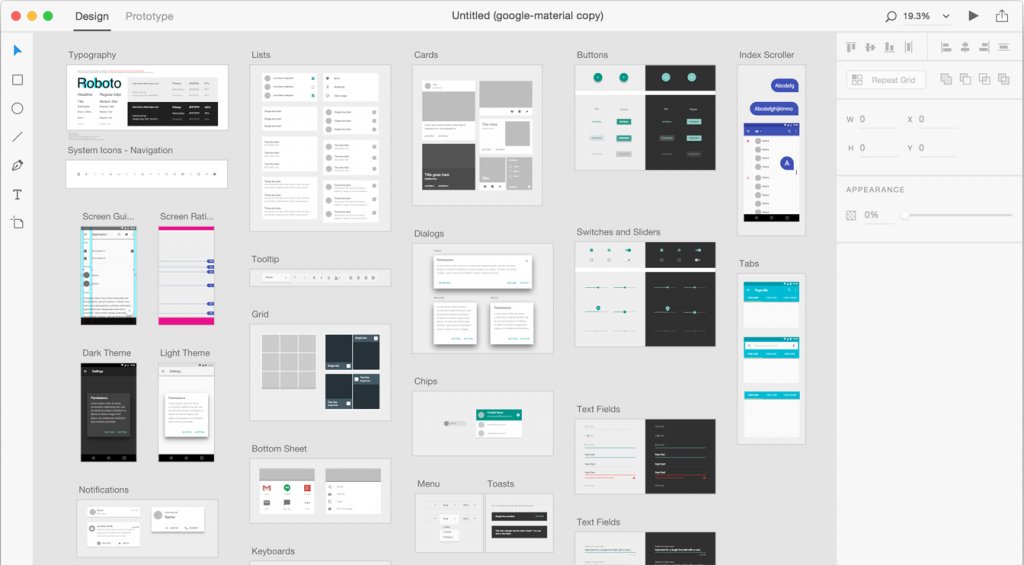
Se você está trabalhando com mockups e wireframes, geralmente você está trabalhando focado no funcionamento em um sistema operacional. Para montar seu leiaute de forma mais simples e sem perder muito tempo se adequando à diretriz escolhida, as desenvolvedoras costumam também disponibilizar UI Kits.
Esses kits de interface de usuário são arquivos ou bibliotecas que possuem os principais elementos gráficos genéricos do sistema. Geralmente é incluído elementos como botões, inputs, padrões de texto, cores, etc. Os principais UI kits, incluindo Android e iOS estão disponíveis direto pelas respectivas empresas ou através das desenvolvedoras dos principais softwares de mockups.
Protótipo
O último passo antes (ou até durante) a implementação é a prototipagem. Basicamente, ele é um passo acima do mockup. Uma etapa onde o designer de interação não apenas demonstra o leiaute per se, mas as ações e interações entre as telas e elementos. Há várias formas de se criar um protótipo.
Algumas pessoas mais experientes preferem criar HTMLs simples, com animações e ações apenas com dados de exemplos, para demonstrar o comportamento, sem se importar ainda com tecnologias ideais ou funcionalidade, pois a ideia é ser apenas demonstrativo.
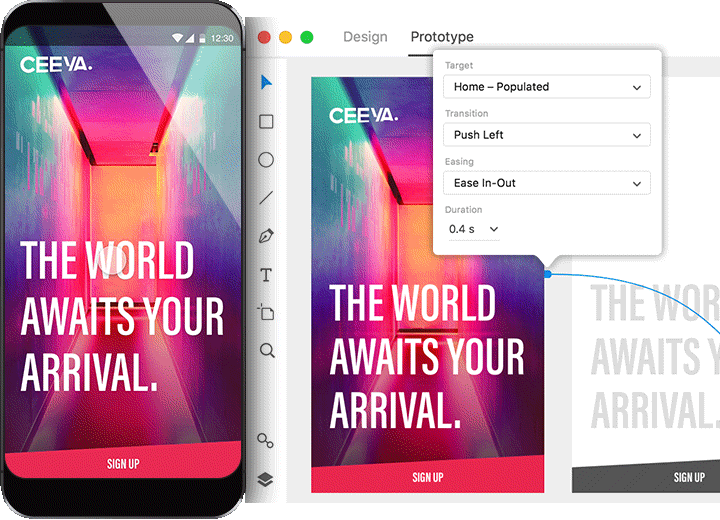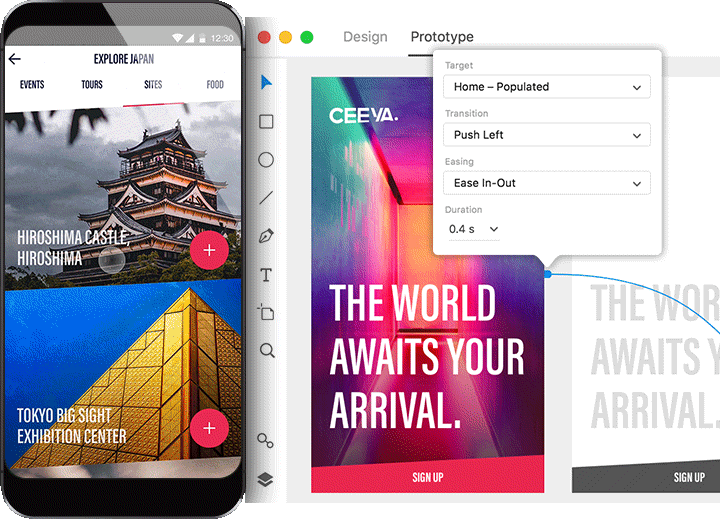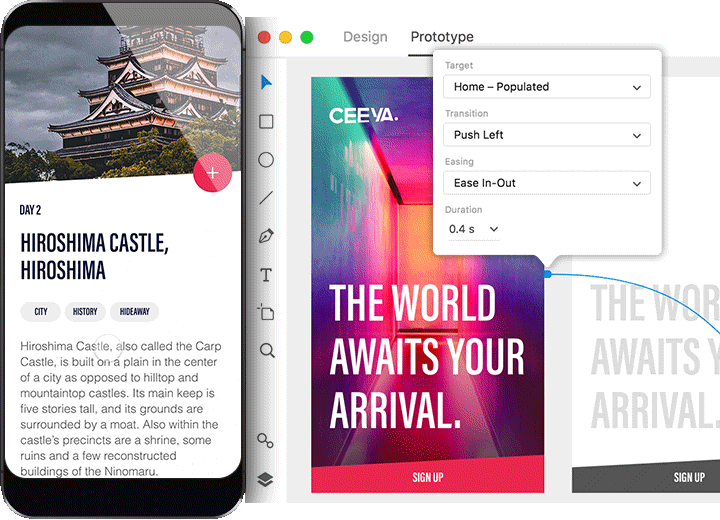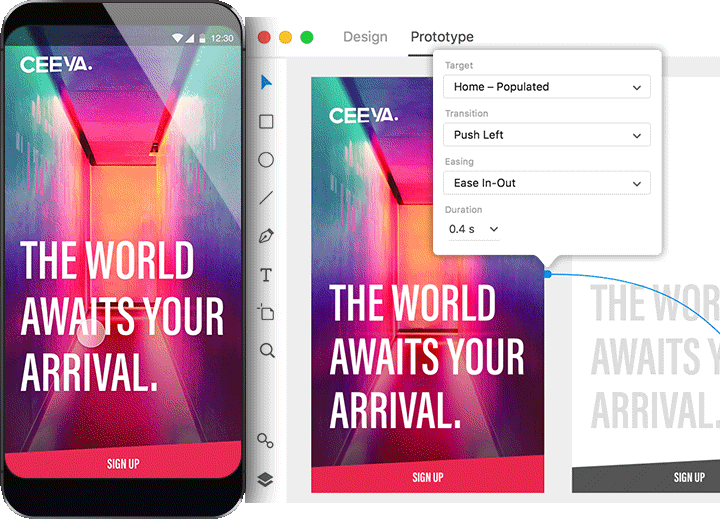
Hoje em dia, entretanto, é mais comum usar ferramentas de prototipagem. Quase todas as ferramentas modernas de mockup também fazem prototipagem, como o Adobe XD, Sketch, Figma, Zeplin, dentre outros. Esses aplicativos possuem diversas ferramentas não só de interação, como demonstração de transições e testes em dispositivos móveis.
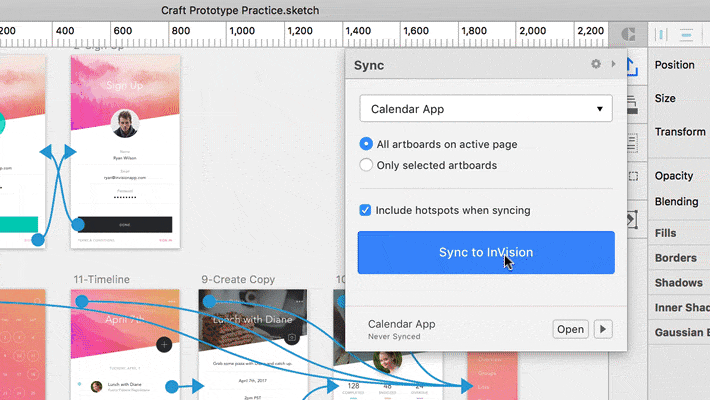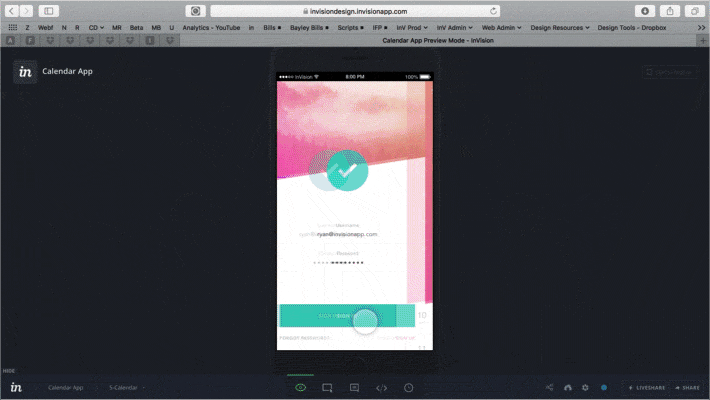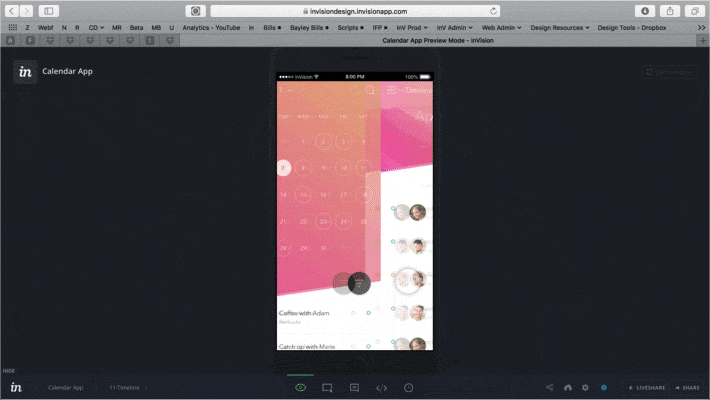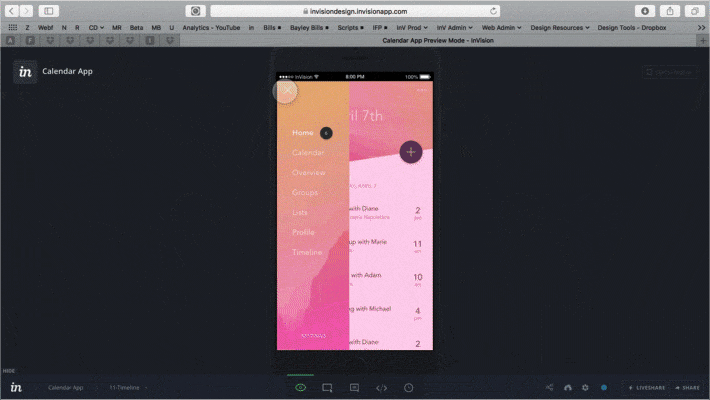
Outra forma de prototipagem são as criadas para apresentação em vídeo. Geralmente são criadas para vender uma ideia e não tem ainda um planejamento do software. Algumas ferramentas de prototipagem, como o InVision, Fuse e o Proto.io possuem ferramentas específicas para exportação em vídeo. Há também quem prefira fazer as transições do protótipo direto no After Effects, para dar um charme a mais para essas apresentações, geralmente com o uso de bibliotecas de animações.
Concluindo
O processo de esquematização visual de uma aplicação é fundamental para que a equipe envolvida no desenvolvimento tenha um guia de como deverá ser projetada a aplicação. Desde o esboço até a prototipagem, essas técnicas ajudam na compreensão, agilidade e segurança do projeto. O esforço para conhecer bem os termos ajuda na comunicação entre os integrantes da equipe, garantindo uma melhor interação entre todos.
Se gostou do que leu, curta a página no Facebook e compartilhe a informação.